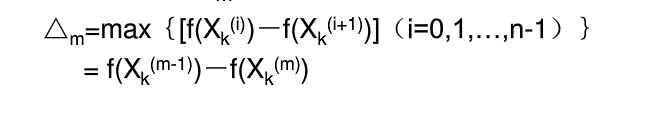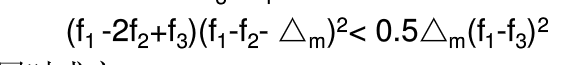鲍威尔法又称方向加速法,它由Powell于1964年提出,是利用共轭方向可以加快收敛速度的性质形成的一种搜索方法。该方法不需要对目标函数进行求导,当目标函数的导数不连续的时候也能应用,因此,鲍威尔算法是一种十分有效的直接搜索法。
Powell法可用于求解一般无约束优化问题,对于维数n<20的目标函数求优化问题,此法可获得较满意的结果。
不同于其他的直接法,Powell法有一套完整的理论体系,故其计算效率高于其他直接法。该方法使用一维搜索,而不是跳跃的探测步。同时,Powell法的搜索方向不一定为下降方向。
设A为n阶实对称正定矩阵,若有两个n维向量S1和S2可以满足S1*AS2=0.则称向量S1与S2对矩阵A共轭,共轭向量的方向称为共轭方向。
设A为n×n阶实对称正定矩阵,Si(i=1,2,3,...,n)是关于A的n个相互共轭的非零向量,对于正定二次函数f(x)的极小化寻优问题,从任何初始点出发,依次沿Si方向经过n次一维搜索即可收敛到极小点X*=X(n)。
沿n元二次正定函数的n个共轭方向进行n次一维搜索就可达到目标函数的极小点。
计算步骤:
Step1:选取初始数据。选取初始点x0,n个线性无关的搜索方向d0,d1,...dn-1,给定允许误差Err,令k>0;
Step2:进行基本搜索。令y0=x1,依次沿d0,d1,...,dn-1进行一维搜索。对一切j=1,2,...,n记f(y(j-1)+λ(j-1)d(j-1)) = min f(y(j-1)+λd(j-1)),
y(j) = y(j-1)+λ(j-1)d(j-1);
Step3:进行加速搜索。取加速方向d(n)=y(n)-y(0);若||d(n)||<Err,迭代终止,得到y(n)为问题的近似最优解;否则,点y(n)出发沿d(n)进行一维搜索,求出λ(n),使得f(y(n)+λ(n)d(n))=min f(y(n)+λd(n)).
记:x(k+1) = y(n)+λ(n)d(n),转Step4.
Step4:调整搜索方向。在原来n个方向d(0),d(1),...,d(n-1)中,除去d0增添d(n),构成新的搜索方向,返回Step2.
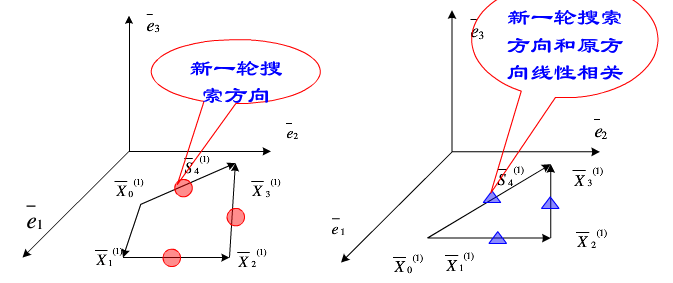
原始的Powell法是沿着逐步产生的共轭方向进行一维搜索的。现在以二维二次目标函数为例来说明。
如上图所示,选定初始点X0(1),初始方向S1(1)=e1=[1,0]';S2(1)=e2=[0,1]';
第一轮循环:
初始点X0(1)---->(e1,e2)---->终点X2(1)---->生成新方向 S(1) = X2(1)-X0(1);
第二轮循环:
初始点X0(2)---->(e2,S(1))---->终点X2(2)---->生成新的方向 S(2) = X2(2)-X0(2);
通过上图我们会发现,点X0(2)、X2(2)是先后两次沿S(1)方向一维搜索到得极小点。由共轭性可以得到:连接X0(2)和X2(2)构成的矢量S(2)与S(1)对H共轭。
从理论上讲,二维二次正定函数经过这组共轭方向的一维搜索,迭代点以达到函数函数的极小值点X*。
将此结构推广至n维二次正定函数,即依次沿n个(S(1),S(2),...,S(n))共轭方向一维搜索就能达到极限值点。
1.原始的Powell算法也是一种共轭方向法,由于它仅仅需要计算目标函数值而不必求导数值。因此Powell算法比普通的共轭方向法(共轭梯度法)更具实用性。
2.原始Powell算法可用于求解一般无约束优化问题。
3.然而,在原始的Powell算法中,必须保持每次迭代中前n搜索方向线性无关,否则将永远得不到问题的最优解。
当某一循环方向组中的矢量系出现线性相关的情况(退化,病态)时,搜索过程在降维的空间进行,致使计算不能收敛而失败。
为了避免此种情况产生,提出了修正的Powell算法。
为了避免鲍威尔法缺陷,Powell提出了相应的修正算法:
和原始的Powell算法的主要区别在于:
1. 在构成第k+1次循环方向组时,不用淘汰前一循环中的第一个方向S1(k)的办法,而是计算函数值,并根据是否满足条件进行计算。
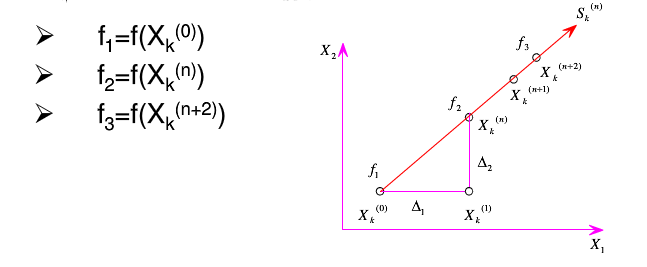
2. 找出前一轮迭代法中函数值下降最多的方向m以及下降量△m,即:
可以证明:若f3<f1;
同时成立。
表明方向Sk(n)与原方向组成线性无关,可以用来替换对象△m所对应的方向Sk(m)。否则仍然用原方向组进行第k+1轮搜索。
Step1:选取初始数据。选取初始点x0,n个线性无关的初始搜索方向d0,d1,...,dn-1;给定允许误差Err>0,令k=0;
Step2:进行基本搜索。令y0=x(k),依次沿d0,d1,...,dn-1进行一维搜索。对一切j=1,2,...,n,记f(y(j-1)+λ(j-1)d(j-1)) = minf(y(j-1)+λd(j-1)), y(j) = f(y(j-1)+λ(j-1)d(j-1)) ;
Step3:检查是否满足终止条件。取加速度方向d(n)=y(n)-y(0);若||d(n)||<Err,迭代终止,得yn为问题的最优解;否则 转Step4。
Step4:确定搜索方向,按照上式公式确定m,若验证式子成立,转Step5;否则,转Step6。
Step5:调整搜索方向。从点yn出发沿方向dn进行一维搜索,求出λn,使得f(yn+λn*dn)=min f(yn+λ*dn);令 x(k+1)=yn+λn*dn。再令d(j)=d(j+1),j=m,m+1,...,n-1.k=k+1,返回Step2。
Step6:不调整搜索方向,令x(k+1)=yn;
k=k+1,返回Step2。
用修正的Powell算法求f(x)=x1*x1+2*x2*x2-4*x1-2*x1*x2的最优解。X0=[1,1]';收敛精度Err=0.001。
解:X0(1)=X0=[1,1]';f1=f(x0(1))=-3;
第一轮进行循环:
沿坐标轴方向向S1=[1,0]方向进行一维搜索:
X1(1) = X0(1)+a(1)*S1(1) = [1,1]'+a1(1)[1,0]'=[1+a1(1),1]'
将X1(1)带入上式,求导可以确定a1(1)=2时,得到极小值。此时,X1(1)=[3,1]; f(X1(1))=-7。
沿坐标轴方向向S2=[0,1]方向进行一维搜索:
X2(1) = X1(1)+a2(1)*S2(1) = [3,1]'+[0,a2(1)]'=[3,1+a2(1)]'。
将X2(1)代入上式,求导可以确定a2(1)=1/2,得到极小值。此时,X2(1)=[3,1.5]; f(X2(1))=-7.5。
检验是否满足终止迭代条件||X2(1)-X0(1)|| = 2.06>Err.
计算各个方向上的函数下降量:
△1=f(X0(1))-f(X1(1))=4;
△2=f(X1(1))-f(X2(1))=0.5;
△m=min{4,0.5}=4;
映射点:
X(1) = 2X2(1)-X0(1)=2*[3,1.5]'-[1,1]=[5,2];
条件验证:f3=f(X(1))=-7, f3<f1
(f1-2f2+f3)(f1-f2-△m)^2 = 1.25 < △m/2*(f1-f3)^2 =32 满足。
因此,得到新的搜索方向:S(1)=X2(1)-X0(1)=[3,1.5]-[1,1]=[2,1.5]';
沿S(1)方向再次做一维搜索:
X3(1)=X2(1)+a3(1)*S(1)=[3,1.5]+a3(1)[2,1.5] = [3+2*a3(1),1.5+1.5a3(1) ];
当a3(1)=0.4时,取得极小值。此时,X3(1)=[19/5,17/10]; f(X3(1)) = -7.9。
以X0(2) = X3(1)作为新的起点,沿(e2,S(1))方向进行一维搜索,开始进入第二个循环:
X2(0)=[19/5,17/10]; f(X2(0))=-7.9;
沿e2=[0,1]方向进行一维搜索:
X1(2) = [19/5,19/10]; f(X1(2))=-7.98
沿S(1)=[2,1.5]方向进行一维搜索:
X2(2) = [99/25,97/50]; f(X2(2)) =-7.996
检验:||X2(2)-X2(0)|| = 0.288>Err
继续进行迭代:△1=0.08;
△2=0.016;
△m=0.08;
映射点:X(2)=2*X2(2)-X0(2)=[103/25,109/50]; f(X(2))=-7.964>f1 条件不满足。
新的方向:S(2)=[99/25,97/50]-[19/5,17/10]=[4/25,12/50];
进行继续迭代时,取X3(0)=X2(2),沿着(e2,S(1))方向一维搜索进行第三轮循环:
X3(1)=[99/25,99/50] ; f1=-7.9992;
X3(2)=[3.9992,1.988]; f2=-7.99984;
检验:||X2(3)-X0(3)||=0.0577 >Err;
X(3)=[4.024,2.036]'; f3=-7.99856; f3>f1.
由于S(1)即S(2)为共轭方向,目标函数是二次函数,若沿S(2)方向进行一维搜索得到
X(2)=[4,2],F(X(2))=-8,此为目标函数的最优解。